各位网友好,小编关注的话题,就是关于为什么会有预备定理的问题,为大家整理了2个问题为什么会有预备定理的解答内容来自网络整理。
相似三角形预备定理
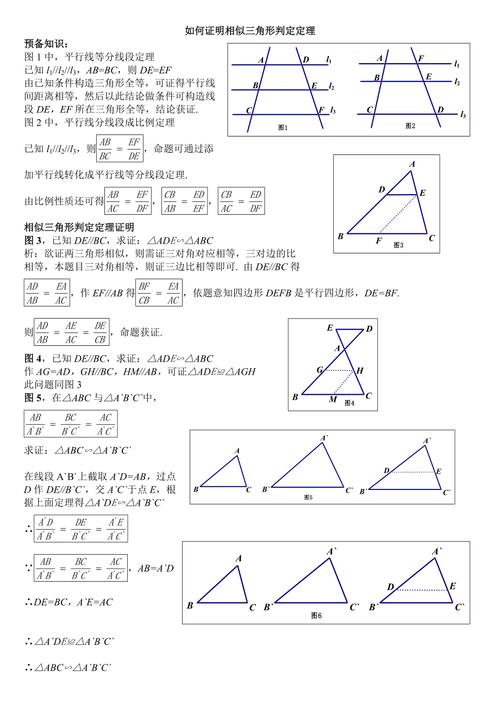
仅用相似三角形的定义证明该定理 相似三角形预备定理:平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例. △ABC,DE‖BC,交AB于D,交AC于E DE‖BC, 同位角相等所以, ∠ADE=∠ABC,∠AED=∠ACB,∠A=∠A, △ABC∽△ADE, AB:AC:BC=AD:AE:DE. 那就用后边的吧: 一条线段与间距相等的一组平行线相交,平行线将该线段等分.——公理还是定理记不请了. 一组平行线与两条线段相交,平分一条线段则平分另一条线段.——也是定理了. 设△ABC,B'C'‖BC,交AB于B',交AC于C', 做一组平行于BC的线段,当然也平行于B'C'了, 过点A做BC的平行线L, 做L和BC的平行线B1C1,使得B1平分AB,则C1平分AC, 看看B1C1和B'C'是否重合, 如果不重合,再做BC的平行线将AB段4等分,看看是否有线和B'C'重合,没有就继续8等分. 如此重复... B'C'与离它最近的平行线之间的距离将越来越小,直到小于任何给定的数值,也就是将趋于无穷小. 这时,AB'之间有m个间隔,B'B之间有n个间隔,则AB':B'B=m:n, 同样,AC'之间有m个间隔,C'C之间有n个间隔,则AC':C'C=m:n, △ABC和△AB'C',∠A=∠A,AB':AB=AC':AC=m:(m+n). 所以 △ABC∽△AB'C', AB:AC:BC=AB':AC':B'C'.

答:相似三角形对应角。对应边等成比例。_一个图形按照一定的比例扩大或缩小得到新的图形与原图形相似。它们对应边的比叫相似比。三角形相似的判定。有两个对应相等,则三角形相似。两边对应成比例,又一夹角相等,则三角形相似。
三边对应成比三角形相似。相似三角形的性质。对应角相等。对应边成比例。周长等于相似比。面和比等相似比的平方。
10什么叫做预备定理
仅用相似三角形的定义证明该定理 相似三角形预备定理:平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例. △ABC,DE‖BC,交AB于D,交AC于E DE‖BC, 同位角相等所以, ∠ADE=∠ABC,∠AED=∠ACB,∠A=∠A, △ABC∽△。
到此,大家对为什么会有预备定理的解答时否满意,希望为什么会有预备定理的2解答对大家有用,如内容不符合请联系小编修改。






